Coordinates, Directions, and Transforms

Overview

Engineering data describes direction vectors, points in space, and transformation matrices. The rosemath library has functions to work with these concepts and application code can build upon them for things specific to STEP, IFC, or CIS/2 geometry.

All definitions are in the rose_xform.h header file.

The functions use arrays of doubles because that is the simplest and most widely applicable form. We have RoseDirection, RosePoint, and RoseXform classes to wrap the arrays with named access and update for clearer coding. They are defined with the exact same memory layout so you can move back and forth as needed.

Points and directions are just double[3]. We have 2D versions of some functions which expect double[2]. The transform functions use a double[16] that follows the GL usage shown below.

m[0-2] is the x axis direction,	 m[3] is zero
m[4-6] is the y axis direction,	 m[7] is zero
m[8-10] is the z axis direction, m[11] is zero
m[12-14] is the origin,		 m[15] is one

double m[16] = {
       xi, xj, xk, 0.0,	 yi, yj, yk, 0.0,
       zi, zj, zk, 0.0,	 wx, wy, wz, 1.0
       };

Be aware that math books, wikipedia, and even GL manuals show the values as a 4x4 matrix in column order (xdir is the first column, ydir is the second column, etc). This is the correct mathematical notation, but can be confusing if you have a mental picture of the double[16] as four rows. Just use the roadmap above and everything will be fine.

There are also 2D transform functions that expect a double[9]. The pattern is similar.

m[0-1] is the x axis direction,	 m[2] is zero
m[3-4] is the y axis direction,	 m[5] is zero
m[6-7] is the origin,		 m[8] is one

double m[9] = {
       xi, xj, 0.0,  yi, yj, 0.0,  wx, wy, 1.0
       };

The functions use the following name prefixes. If there are 2D versions, they are named as shown with an extra "2d" in the name

rose_pt_ 3D points
rose_pt2d_ 2D points
rose_vec_ 3D values, points or directions
rose_vec2d_ 2D values, points or directions
rose_xform_ 3D transform or axis placement
rose_xform2d_ 2D transform or axis placement

The following simple C++ classes wrap the arrays to make code easier to understand. They only provide named access to the elements. eg. x() instead of m[0]. All complex calculations are done by separate standalone functions. Everything is public so you can use the class with an array function by just passing the ".m" member.

The C++ compiler provides copy operatiors and temp object creation, so you can use these to pass a copy of transform, direction, or point data back from your functions.

The classes have no virtual fuctions, so the memory layout of the class is identical to the array. This lets us reinterpret cast an existing array to a class reference if needed, as seen in RoseXform::xdir()

RosePoint wraps a double[3] for a 3D point
RosePoint2D wraps a double[2] for a 2D point
RoseDirection wraps a double[3] for a 3D direction vector
RoseDirection2D wraps a double[2] for a 2D direction vector
RoseXform wraps a double[16] for a 3D transform matrix
RoseXform2D wraps a double[9] for a 2D transform matrix

Array Constants

const double rose_vec_zero[3] = {0, 0, 0};

const double rose_vec_100[3] = {1, 0, 0};
const double rose_vec_010[3] = {0, 1, 0};
const double rose_vec_001[3] = {0, 0, 1};

const double rose_xform_identity[16];
const double rose_xform2d_identity[9];

These constant arrays are initialized to the origin, cardinal axis directions, and identity matrix. You can use them instead of literal values for convenient testing and initialization.

double xf[16];

rose_put_vec_xdir(xf, rose_vec_100);	// with const
rose_put_vec_xdir(xf, 1, 0, 0);		// explicit vals

double vec[3];

if (rose_vec_is_equal(vec, rose_vec_001))
   printf(Aligned with the Z-axis\n);

if (rose_vec_is_equal(vec, 0, 0, 1))	// explicit vals
   printf(Aligned with the Z-axis\n);

Matrix Macros

// macros to find the right part of the double[16]
#define ROSE_XFORM_XDIR(a)	(a)
#define ROSE_XFORM_YDIR(a)	((a)+4)
#define ROSE_XFORM_ZDIR(a)	((a)+8)
#define ROSE_XFORM_ORIGIN(a)	((a)+12)

// macros to find the right part of the double[9]
#define ROSE_XFORM2D_XDIR(a)	(a)
#define ROSE_XFORM2D_YDIR(a)	((a)+3)
#define ROSE_XFORM2D_ORIGIN(a)	((a)+6)

// macros to simplify initializing transform arrays
#define ROSE_XFORM_IDENTITY	{ 1, 0, 0, 0,	0, 1, 0, 0,   0, 0, 1, 0,   0, 0, 0, 1 }
#define ROSE_XFORM2D_IDENTITY	{ 1, 0, 0,  0, 1, 0,  0, 0, 1 }

These macros simplify access to the different parts of the double[16] array for a transform. Using them instead of raw index values will clarify the intent of your code. You can add an index for the ijk or xyz values as shown below. The XFORM2D versions work on the double[9] array for a 2D transform.

The ROSE_XFORM_IDENTITY and ROSE_XFORM2D_IDENTITY macros are an efficient way to initialize an array variable for a 3D or 2D transform. It only works for initialization, other places can call rose_xform_put_identity() or use the rose_xform_identity array constant.

double xf[16] = ROSE_XFORM_IDENTITY;

double x_coord = ROSE_XFORM_ORIGIN(xf)[0];
double y_coord = ROSE_XFORM_ORIGIN(xf)[1];
double z_coord = ROSE_XFORM_ORIGIN(xf)[2];

rose_poly2d_area()

double rose_poly2d_area(
	RoseReal2DArray &polygon
	);

The rose_poly2d_area() function computes the area of a closed polygon in the XY plane. The first point should not be repeated as the last point, but this function will work either way.

The area value will be positive if the points are in mathematically positive order (counter clockwise, looking down into the XY plane), and negative if they are reversed.

rose_poly2d_is_inside()

int rose_poly2d_is_inside(
	RoseReal2DArray &polygon,
	const double test_pt[2]
	);

The rose_poly2d_is_inside() function returns non-zero if a point is within a closed polygon in the XY plane. The first point of the polygon should not be repeated as the last point.

rose_pt_circle_params()

int rose_pt_circle_params (
	double center[3],
	double &radius,
	double axis_dir[3],
	const double p1[3],
	const double p2[3],
	const double p3[3]
	);

int rose_pt_circle_params (
	RosePoint& center,
	double &radius,
	RoseDirection& axis,
	const RosePoint& p1,
	const RosePoint& p2,
	const RosePoint& p3
	);

The rose_pt_circle_params() function takes three points and attempts to fit them to an arc. The function returns nonzero on success and passes pack the center coordinates, the radius, and the normalized axis direction for the circle. The function returns zero If the points can not be fit to an arc.

rose_pt_distance()

double rose_pt_distance(
	const double p1[3],
	const double p2[3]
	);

double rose_pt2d_distance(
	const double p1[2],
	const double p2[2]
	);

The rose_pt_distance() function finds the distance between a pair of points. The rose_pt2d_distance() version operates on 2D points.

double p1[] = { 0.0, 0.0. 1.0 };
double p2[] = { 0.0, 0.0. 5.0 };

// should return 4.0
double dist = rose_pt_distance(p1, p2);

rose_pt_distance_sq()

double rose_pt_distance_sq(
	const double p1[3],
	const double p2[3]
	);

double rose_pt2d_distance_sq(
	const double p1[2],
	const double p2[2]
	);

The rose_pt_distance_sq() function finds the squared distance between a pair of points. This avoids the square root operation done by rose_pt_distance() if the situation does not reqire it. The rose_pt2d_distance_sq() version operates on 2D points.

rose_pt_midpoint()

void rose_pt_midpoint(
	double result[3],
	const double p1[3],
	const double p2[3]
	);
void rose_pt_midpoint(
	RosePoint& result,
	const RosePoint& p1,
	const RosePoint& p2
	);

void rose_pt2d_midpoint(
	double result[2],
	const double p1[2],
	const double p2[2]
	);
void rose_pt2d_midpoint(
	RosePoint2D& result,
	const RosePoint2D& p1,
	const RosePoint2D& p2
	);

The rose_pt_midpoint() function finds the midpoint on the line connecting two points. The rose_pt2d_midpoint() version operates on 2D points.

RosePoint p1(-1,1,0);
RosePoint p2(5,5,5);
RosePoint ret;

rose_pt_midpoint(ret,p1,p2);
// ret point now contains (2, 3, 2.5)

rose_pt_nearest_on_line()

void rose_pt_nearest_on_line(
	double pt_result[3],
	double * t_result,
	const double zeropt[3],	 // point at t=0
	const double dirvec[3],
	const double testpt[3]
	);

void rose_pt_nearest_on_line(
	RosePoint& pt_result,
	double * t_result,
	const RosePoint& zeropt,  // point at t=0
	const RoseDirection& dirvec,
	const RosePoint& testpt
	);



void rose_pt2d_nearest_on_line(
	double pt_result[2],
	double * t_result,
	const double zeropt[2],	 // point at t=0
	const double dirvec[2],
	const double testpt[2]
	);

void rose_pt2d_nearest_on_line(
	RosePoint2D& pt_result,
	double * t_result,
	const RosePoint2D& zeropt,  // point at t=0
	const RoseDirection2D& dirvec,
	const RosePoint2D& testpt
	);

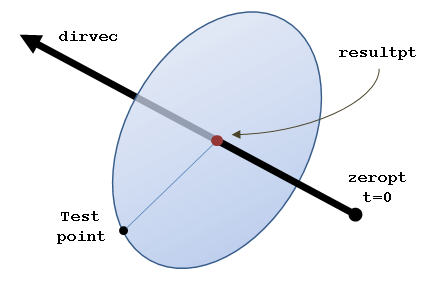
The rose_pt_nearest_on_line() function finds the point on a line nearest to a test point. The function writes the XYZ coordinates to the pt_result array and writes the corresponding T param from the parametric equation of the line to the variable pointed to by t_result. The rose_pt2d_nearest_on_line() function finds the point nearest to a 2D line.

The equation of the line can be written using column vectors. The XYZ value of each point is given by a t parameter, a direction vector (dirvec) and an origin point (zeropt) which is the value when t=0.

(x,y,z) = (zeropt) + t * (dirvec)

If you are not interested in the parametric representation, you can pass a null pointer to t_result and the zeropt can be any point on the line. The distance from the line is found by comparing the pt_result and testpt as shown in the eamples below.

RosePoint zp1(0,0,0);
RosePoint zp2(10,10,0);
RoseDirection dir(1,1,0);

RosePoint test(0,2,0);
RosePoint ret;
double t;

// returns (1,1) and t=1
rose_pt_nearest_on_line(ret, &t, zp1, dir, test);

// returns (1,1) and t= -9
rose_pt_nearest_on_line(ret, &t, zp2, dir, test);

// distance from the line.
double dist = rose_pt_distance (ret, test);

rose_pt_nearest_on_line_thru_pts()

void rose_pt_nearest_on_line_thru_pts(
	double pt_result[3],
	double * t_result,
	const double t_zeropt[3], // point at t=0
	const double t_onept[3],  // point at t=1 
	const double testpt[3]
	);

void rose_pt_nearest_on_line_thru_pts(
	RosePoint& pt_result,
	double * t_result,
	const RosePoint& t_zeropt,     // point at t=0
	const RosePoint& t_onept,      // point at t=1
	const RosePoint& testpt
	);


void rose_pt2d_nearest_on_line_thru_pts(
	double pt_result[2],
	double * t_result,
	const double t_zeropt[2], // point at t=0
	const double t_onept[2],  // point at t=1 
	const double testpt[2]
	);

void rose_pt2d_nearest_on_line_thru_pts(
	RosePoint2D& pt_result,
	double * t_result,
	const RosePoint2D& t_zeropt,  // point at t=0
	const RosePoint2D& t_onept,   // point at t=1
	const RosePoint2D& testpt
	)

The rose_pt_nearest_on_line_thru_pts() function finds the point on a line nearest to a test point. As with rose_pt_nearest_on_line(), the function writes the XYZ coordinates to the pt_result array and writes the corresponding T param from the parametric equation of the line to the variable pointed to by t_result. This function specifies the line as two points. The parameter value is computed by assuming that the t_zeropt is where t=0 and t_onept is where t=1.

The function considers the entire infinite line, and not just the segment between t_zeropt and t_onept. The closest point is on the line segment if 0. <= *t_result <= 1.

If you are not interested in the parametric representation, you can pass a null pointer to t_result and the zeropt can be any point on the line.

The rose_pt2d_nearest_on_line_thru_pts() function finds the point nearest to a 2D line.

rose_pt_nearest_on_plane()

void rose_pt_nearest_on_plane(
	double pt_result[3],
	double * dist_result,
	const double origin[3],  // plane origin
	const double normal[3],
	const double testpt[3] 
	);

void rose_pt_nearest_on_plane(
	RosePoint& pt_result,
	double * dist_result,
	const RosePoint& origin,  // plane origin
	const RoseDirection& normal,
	const RosePoint& testpt
	);

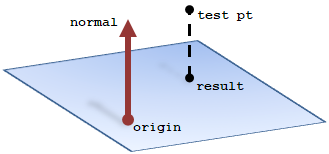
The rose_pt_nearest_on_plane() function projects a point onto to the plane defined by an origin and normal.

The function passes back the projected point and distance between the test point and projected point along the normal. This distance will be negative if the original point is on the side of the plane opposite the normal.

RosePoint zp1(0,0,0);
RoseDirection zdir(0,0,1);
RosePoint ret;
double dist;

RosePoint t1(25,50,75);
rose_pt_nearest_on_plane(ret, &dist, zp1, zdir, t1);
// ret point is (25, 50, 0) with dist = 75


RosePoint t2(25,50,-75);
rose_pt_nearest_on_plane(ret, &dist, zp1, zdir, t2);
// ret point is (25, 50, 0) with dist = -75

rose_pt_nearest_on_plane_uv()

void rose_pt_nearest_on_plane_uv(
	double pt_result[3],
	double * u_result,
	double * v_result,
	const double plane_ap3d[16],
	const double testpt[3]
	);

void rose_pt_nearest_on_plane_uv(
	RosePoint& pt_result,
	double * u_result,
	double * v_result,
	const RoseXform& xf,
	const RosePoint& testpt
	);

The rose_pt_nearest_on_plane_uv() function projects a point onto to the plane defined by an axis placement.

The function passes back the projected point and the U/V solution of the plane equation, where U is along the X-axis and V is along the Y-axis defined by the axis placement.

Plane(u,v) = (location) + u(xdir) + v(ydir)

RoseXform xf1;
double u, v;

RosePoint t1(25,50,75);
rose_pt_nearest_on_plane_uv(ret, &u, &v, xf1, t1);
// ret point is (25, 50, 0) with u/v = 25/50

RosePoint t2(25,50,-75);
rose_pt_nearest_on_plane_uv(ret, &u, &v, xf1, t2);
// ret point is (25, 50, 0) with u/v = 25/50


RoseXform xf2;
RosePoint zp2(20,30,0);
xf2.origin(zp2);  // change the origin of the plane

rose_pt_nearest_on_plane_uv(ret, &u, &v, xf2, t1);
// ret point is (25, 50, 0) with u/v = 5/20

rose_pt_on_line_and_plane()

int rose_pt_on_line_and_plane(
	double pt_result[3],
	double * t_result,
	const double linept[3],	 // point at t=0
	const double linedir[3],
	const double planept[3],
	const double planenorm[3]
	);

The rose_pt_on_line_and_plane() function computes the intersection point between a line and a plane. The function returns zero if the line and point are parallel and there is no single point intersection. It returns non-zero if a single point is found and the coordinates are placed in the pt_result array. If a non-null t_result pointer is given, the T parameter for the line will be placed in that location.

If no solution is found and it is important to know whether the line lies in the plane rather than just being parallel, find the difference between the line and plane points and see if the dot product with the plane normal is zero.

rose_vec_cross()

void rose_vec_cross(
	double result[3],
	const double vec1[3],
	const double vec2[3]
	);
void rose_vec_cross(
	RosePoint& result,
	const RosePoint& vec1,
	const RosePoint& vec2
	);
void rose_vec_cross(
	RoseDirection& result,
	const RoseDirection& vec1,
	const RoseDirection& vec2
	);


// 2D version, note different return type
double rose_vec2d_cross(
	const double vec1[2],
	const double vec2[2]
	);
double rose_vec2d_cross(
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	);
double rose_vec2d_cross(
	const RoseDirection2D& vec1,
	const RoseDirection2D& vec2
	);

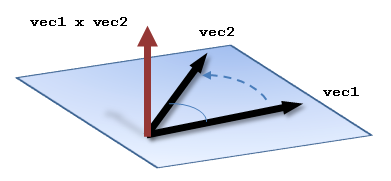
The rose_vec_cross() function calculates the cross product of two vectors (vec1 × vec2) and copies the resulting vector to result. The cross product produces a vector perpendicular to the plane formed by the two input vectors, with the direction given by the right hand rule

The rose_vec2d_cross() function calculates the cross product of a pair of 2D vectors, but unlike other 2D functions, this will produce a 3D result. In this case, the result will be a vector either into or out of the 2D plane. Since the i and j elements of that vector will always be zero, rose_vec2d_cross just returns the k value directly as a double.

rose_vec_det2x2()

double rose_vec_det2x2(
	const double v1[2],
	const double v2[2]
	);

double rose_vec_det2x2(
	const RoseDirection2D& d1,
	const RoseDirection2D& d2
	);

The rose_vec_det2x2() function computes the determinant of a 2x2 matrix formed from a pair of two element arrays. There is also an overload that accepts RoseDirection2D. See rose_vec_det3x3() for the 3x3 matrix version.

rose_vec_det3x3()

double rose_vec_det3x3(
	const double v1[3],
	const double v2[3],
	const double v3[3]
	);

double rose_vec_det3x3(
	const RoseDirection& d1,
	const RoseDirection& d2,
	const RoseDirection& d3
	);

The rose_vec_det3x3() function calculates the determinant of a 3x3 matrix formed from three arrays that each have three elements. The determinant of a 3x3 matrix can be used to find the volume of space enclosed by three vectors.

There is also an overload that accepts RoseDirection. See rose_vec_det2x2() for the 2x2 matrix version. The rose_xform_det() function calculates the determininant of transforms as 3x3 and 4x4 matrices.

rose_vec_diff()

void rose_vec_diff(
	double result[3],
	const double vec1[3],
	const double vec2[3]
	);
void rose_vec_diff(
	RosePoint& result,
	const RosePoint& vec1,
	const RosePoint& vec2
	);
void rose_vec_diff(
	RoseDirection& result,
	const RosePoint& vec1,
	const RosePoint& vec2
	);
void rose_vec_diff(
	RoseDirection& result,
	const RoseDirection& vec1,
	const RoseDirection& vec2
	);


void rose_vec2d_diff(
	double result[2],
	const double vec1[2],
	const double vec2[2]
	);
void rose_vec2d_diff(
	RosePoint2D& result,
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	);
void rose_vec2d_diff(
	RoseDirection2D& result,
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	);
void rose_vec2d_diff(
	RoseDirection2D& result,
	const RoseDirection2D& vec1,
	const RoseDirection2D& vec2
	);

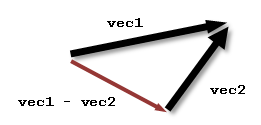
The rose_vec_diff() function does simple vector subtraction. The result is a vector that is equivalent to "vec1" minus the "vec2". If you are combining unit direction vectors, you must call rose_vec_normalize() to normalize the result in a separate step. The rose_vec2d_diff() function is a 2D version.

double a[3] = { 40, 50, 60 }
double b[3] = { 1, 2, 3 }
double c[3];

// c = a - b  results in c = (39, 48, 57)
rose_vec_diff(c, a, b);

// c = a, followed by c -= b  results in c = (39, 48, 57)
rose_vec_put(c, a);
rose_vec_diff(c, c, b);

rose_vec_dot()

double rose_vec_dot(
	const double vec1[3],
	const double vec2[3]
	);
double rose_vec_dot(
	const RosePoint& vec1,
	const RosePoint& vec2
	);
double rose_vec_dot(
	const RoseDirection& vec1,
	const RoseDirection& vec2
	);


double rose_vec2d_dot(
	const double vec1[2],
	const double vec2[2]
	);
double rose_vec2d_dot(
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	);
double rose_vec2d_dot(
	const RoseDirection2D& vec1,
	const RoseDirection2D& vec2
	);

The rose_vec_dot() function calculates the dot product of two vectors (vec1 ⋅ vec2). The dot product is the length of the projection of the first vector upon the second, which is can be found by multiplying the length of the first vector by the cosine of the angle between them. The rose_vec2d_dot() function calculates the dot product for a pair of 2D vectors.

rose_vec_is_equal()

int rose_vec_is_equal(
	const double vec1[3],
	const double vec2[3],
	double tol=ROSE_EPSILON
	);
int rose_vec_is_equal(
	const double vec1[3],
	double i,
	double j,
	double k,
	double tol=ROSE_EPSILON
	);
int rose_vec_is_equal(
	const RosePoint& vec1,
	const RosePoint& vec2
	double tol=ROSE_EPSILON
	);
int rose_vec_is_equal(
	const RoseDirection& vec1,
	const RoseDirection& vec2
	double tol=ROSE_EPSILON
	);


int rose_vec2d_is_equal(
	const double vec1[2],
	const double vec2[2],
	double tol=ROSE_EPSILON
	);
int rose_vec2d_is_equal(
	const double vec1[3],
	double i,
	double j,
	double tol=ROSE_EPSILON
	);
int rose_vec2d_is_equal(
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	double tol=ROSE_EPSILON
	);
int rose_vec2d_is_equal(
	const RoseDirection2D& vec1,
	const RoseDirection2D& vec2
	double tol=ROSE_EPSILON
	);

The rose_vec_is_equal() function returns true if each element in pair of three element arrays are equal to each other. That is to say the first elements in both arrays are equal, the second elements are equal, and the third elements are equal. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use ROSE_EPSILON. The rose_vec2d_is_equal() function is a 2D version.

There is also versions of the function that takes the components as individual numbers instead of an array. This makes code clearer when testing for literal directions like (0,0,1) or (1,0,0). There is only one overload with this signature so when using with a RosePoint or RoseDirection, just pass the ".m" array element.

RosePoint p1 (1, 2, 3);
RosePoint p2 (4, 5, 6);
RosePoint p3 (1, 2, 3 + (ROSE_EPSILON/2.0));
RosePoint p4 (1, 2, 3 + (2*ROSE_EPSILON));

if (!rose_vec_is_equal(p1, p2)) {
     printf(not equal, vals are very different\n);
}

if (rose_vec_is_equal(p1, p3)) {
     printf(these are equal, only a half-epsilon apart\n);
}

if (!rose_vec_is_equal(p1, p4)) {
     printf(not equal, more than an epsilon apart\n);
}

if (rose_vec_is_equal(p1, p4, 3.0*ROSE_EPSILON)) {
     printf(now they are equal, because we use a larger epsilon\n);
}


RoseDirection d1(0,0,1);
if (!rose_vec_is_equal(d1, 1, 0, 0)) {
     printf(direction along x axis\n);
}

rose_vec_is_zero()

int rose_vec_is_zero(
	const double vec[3],
	double tol=ROSE_EPSILON
	);
int rose_vec_is_zero(
	const RosePoint& vec,
	double tol=ROSE_EPSILON
	);
int rose_vec_is_zero(
	const RoseDirection& vec,
	double tol=ROSE_EPSILON
	);


int rose_vec2d_is_zero(
	const double vec[2],
	double tol=ROSE_EPSILON
	);
int rose_vec2d_is_zero(
	const RosePoint2D& vec,
	double tol=ROSE_EPSILON
	);
int rose_vec2d_is_zero(
	const RoseDirection2D& vec,
	double tol=ROSE_EPSILON
	);

The rose_vec_is_zero() function returns true if each element in a three element array is zero. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use ROSE_EPSILON. This function is equivalent to calling rose_vec_is_equal() to compare an array with (0,0,0). The rose_vec2d_is_zero() function is a 2D version.

RosePoint p1 (0, 0, 0);
RosePoint p2 (4, 5, 6);
RosePoint p3 (0, 0, (ROSE_EPSILON/2.0));
RosePoint p4 (0, 0, (2*ROSE_EPSILON));

if (rose_vec_is_zero(p1)) {
     printf(exactly zero\n);
}

if (!rose_vec_is_zero(p2)) {
     printf(not zero, vals are very different\n);
}

if (rose_vec_is_zero(p3)) {
     printf(zero, within a half-epsilon\n);
}

if (!rose_vec_is_zero(p4)) {
     printf(not zero, more than an epsilon away\n);
}

if (rose_vec_is_zero(p4, 3.0*ROSE_EPSILON)) {
     printf(now considered zero with a larger epsilon\n);
}

rose_vec_length()

double rose_vec_length (const double v[3]);
double rose_vec_length (const RoseDirection& v);

double rose_vec2d_length (const double v[2]);
double rose_vec2d_length (const RoseDirection2D& v);

The rose_vec_length() function returns the length, also called the magnitude, of a vector. The function takes an array[3] of doubles or a reference to a RoseDirection. The rose_vec2d_length() function is a 2D version.

double v1[] = { 0.0, 0.0, 5.0 };
double v2[] = { 30/ROSE_SQRT_3, 30/ROSE_SQRT_3, 30/ROSE_SQRT_3 };

printf (mag1 = %g\n, rose_vec_length(v1));	// prints 5
printf (mag2 = %g\n, rose_vec_length(v2));	// prints 30

RoseDirection dir1(v1), dir2(v2);

printf (mag1 = %g\n, rose_vec_length(dir1)); // prints 5
printf (mag2 = %g\n, rose_vec_length(dir2)); // prints 30

rose_vec_negate()

void rose_vec_negate(
	double result[3],
	const double vec1[3]
	);
void rose_vec_negate(
	RosePoint& result,
	const RosePoint& vec1
	);
void rose_vec_negate(
	RoseDirection& result,
	const RoseDirection& vec1
	);

// Negate in place
void rose_vec_negate (double result[3]) {
void rose_vec_negate (RosePoint& result) {
void rose_vec_negate (RoseDirection& result) {

// 2D versions
void rose_vec2d_negate(
	double result[2],
	const double vec1[2]
	);
void rose_vec2d_negate(
	RosePoint2D& result,
	const RosePoint2D& vec1
	);
void rose_vec2d_negate(
	RoseDirection2D& result,
	const RoseDirection2D& vec1
	);

void rose_vec2d_negate (double result[2]) {
void rose_vec2d_negate (RosePoint2D& result) {
void rose_vec2d_negate (RoseDirection2D& result) {

The rose_vec_negate() function reverses the i,j,k components of a vector so that it points in the opposite direction. The new vector is -i,-j,-k.

The results are always copied to the first argument. Pass one argument if you want to negate in place or two arguments if you want the results put in a different place. The rose_vec2d_negate() function is a 2D version.

double a[3] = { 10, 20, 30 };
double tmp[3];

// tmp will contain (-10, -20, -30)
rose_vec_negate(tmp, a);

// negate in place so "a" will contain (-10, -20, -30)
rose_vec_negate(a);

rose_vec_normalize()

// normalize and assign
void rose_vec_normalize(
	double result[3],
	const double vec[3]
	);
void rose_vec_normalize(
	RoseDirection& result,
	const RoseDirection& vec
	);

// normalize in place
void rose_vec_normalize( double result[3] );
void rose_vec_normalize( RoseDirection& result );


// 2D variations
void rose_vec2d_normalize(
	double result[2],
	const double vec[2]
	);

void rose_vec2d_normalize(
	RoseDirection2D& result,
	const RoseDirection2D& vec
	);

void rose_vec2d_normalize( double result[2] );
void rose_vec2d_normalize( RoseDirection2D& result );

The rose_vec_normalize() function scales the i,j,k components of a vector so that it is a unit vector (length = 1). If the length is smaller than ROSE_EPSILON, all components will be set to zeros. The results are always copied to the first argument. Pass one argument if you want to normalize in place or two arguments if you want the results put in a different place. The rose_vec2d_normalize() function is a 2D version.

double a[3] = { 0, 0, 90 };
double tmp[3];

// tmp will contain (0, 0, 1)
rose_vec_normalize(tmp, a);

// normalize in place so "a" will contain (0, 0, 1)
rose_vec_normalize(a);

rose_vec_normal_to()

void rose_vec_normal_to(
	double result[3],
	const double vec[3]
	);
void rose_vec_normal_to(
	RosePoint& result,
	const RosePoint& vec
	);
void rose_vec_normal_to(
	RoseDirection& result,
	const RoseDirection& vec
	);


void rose_vec2d_normal_to(
	double result[2],
	const double vec[2]
	);
void rose_vec2d_normal_to(
	RosePoint2D& result,
	const RosePoint2D& vec
	);
void rose_vec2d_normal_to(
	RoseDirection2D& result,
	const RoseDirection2D& vec
	);

The rose_vec_normal_to() function finds a vector at right angles to a given vector. There are an infinite number of such normal vectors in 3D, and the function will select one.

The rose_vec2d_normal_to() version returns a unique solution. It takes a 2D direction vector and returns the vector rotated +90° from it in the plane. If you view the input vector as the direction of the X axis, the result will be the direction of the Y axis.

rose_vec_put()

void rose_vec_put(
	double result[3],
	const double src[3]
	);
void rose_vec_put  (
	double result[3],
	double i, double j, double k
	);
void rose_vec_put  (
	double result[3],
	ListOfDouble * lst
	);
void rose_vec_put  (
	double result[3],
	const RoseDirection& vec
	);
void rose_vec_put  (
	double result[3],
	const RosePoint& vec
	);

void rose_vec2d_put(
	double result[2],
	const double src[2]
	);
void rose_vec2d_put(
	double result[2],
	double i, double j
	);
void rose_vec2d_put(
	double result[2],
	ListOfDouble * lst
	);
void rose_vec2d_put(
	double result[2],
	const RoseDirection2D& vec
	);
void rose_vec2d_put(
	double result[2],
	const RosePoint2D& vec
	);

The rose_vec_put() function just encapsulates an assignment to all three elements of an array. The rose_vec2d_put() function is a 2D version that assigns the first two elements of an array. The functions have overloads that take another array, individual values, or a ListOfDouble. The ListOfDouble class is used for the coordinates and direction components in STEP and IFC definitions. Zeros will be used as needed if the list is null or does not contain enough elements.

When working with the RoseDirection, RosePoint, and RoseXform classes, you can just use simple assignment with a object or array and the C++ compiler will use a copy constructor to do the right thing. The rose_vec_put() function is only needed when working with two plain arrays or copying from an object to an array.

double a[3] = { 1, 2, 3 }; 
double b[3] = { 4, 5, 6 };

rose_vec_put(a,b);  // a now contains 4,5,6

a[0]=b[0];	// same thing
a[1]=b[1];
a[2]=b[2];

// with the class wrappers, C++ handles the copy
RosePoint pa ( 1, 2, 3 );
RosePoint pb ( 4, 5, 6 );

pa = pb;    // a now contains 4,5,6
pa = b;	    // copy ctor will even copy the plain array

// copying back to an array requires the function, though
rose_vec_put(b,pa.m);

rose_vec_put_as_unit()

int rose_vec_put_as_unit(
    double res[3],
    const double src[3],
    RoseUnit as_is, 
    RoseUnit to_be
    );

int rose_vec2d_put_as_unit(
    double res[2],
    const double src[2],
    RoseUnit as_is, 
    RoseUnit to_be
    );

The rose_vec_put_as_unit() function copies three elements of an array of doubles and multiplies each element value by a unit conversion factor. The function returns nonzero on success, or zero if there was an error, like not finding a conversion between the units. On error, the result array will be set to all zeros.

The rose_vec2d_put_as_unit() function is a 2D version that assigns the first two elements of an array.

double a[3] = { 1, 2, 3 }; 
double b[3];

// copy a to b and convert from inch to millimeter
// b will contain 1*25.4, 2*25.4, 3*25.4
rose_vec_put_as_unit(b, a, roseunit_in, roseunit_mm);

rose_vec_put_zero()

void rose_vec_put_zero  ( double result[3] );
void rose_vec2d_put_zero( double result[2] );

The rose_vec_put_zero() function assigns zeros to all three elements of the array. The rose_vec2d_put_zero() function is a 2D version that zeros the first two elements of an array. The following are both equivalent pieces of code:

double a[3] = { 1, 2, 3 }; 

rose_vec_put_zero(a);  // a now contains 0,0,0

a[0]=0;		// same thing
a[1]=0;
a[2]=0;

rose_vec_scale()

void rose_vec_scale(
	double result[3],
	const double vec[3],
	double scale
	);
void rose_vec_scale(
	RosePoint& result,
	const RosePoint& vec,
	double scale
	);
void rose_vec_scale(
	RoseDirection& result,
	const RoseDirection& vec,
	double scale
	);



void rose_vec2d_scale(
	double result[2],
	const double vec[2],
	double scale
	);
void rose_vec2d_scale(
	RosePoint2D& result,
	const RosePoint2D& vec,
	double scale
	);
void rose_vec2d_scale(
	RoseDirection2D& result,
	const RoseDirection2D& vec,
	double scale
	);

The rose_vec_scale() function multiplies a scalar constant C to the i,j,k components of a vector. The new vector is C*i,C*j,C*k.

The results are always copied to the first argument. The rose_vec2d_scale() function is a 2D version.

double a[3] = { 10, 20, 30 };
double tmp[3];

// tmp will contain (50, 100, 150)
rose_vec_scale(tmp, a, 5);

// scale in place so "a" will contain (50, 100, 150)
rose_vec_scale(a, a, 5);

rose_vec_sum()


void rose_vec_sum(
	double result[3],
	const double vec1[3],
	const double vec2[3]
	);
void rose_vec_sum(
	RosePoint& result,
	const RosePoint& vec1,
	const RosePoint& vec2
	);
void rose_vec_sum(
	RosePoint& result,
	const RosePoint& vec1,
	const RoseDirection& vec2
	);
void rose_vec_sum(
	RoseDirection& result,
	const RoseDirection& vec1,
	const RoseDirection& vec2
	);


void rose_vec2d_sum(
	double result[2],
	const double vec1[2],
	const double vec2[2]
	);
void rose_vec2d_sum(
	RosePoint2D& result,
	const RosePoint2D& vec1,
	const RosePoint2D& vec2
	);
void rose_vec2d_sum(
	RosePoint2D& result,
	const RosePoint2D& vec1,
	const RoseDirection2D& vec2
	);
void rose_vec2d_sum(
	RoseDirection2D& result,
	const RoseDirection2D& vec1,
	const RoseDirection2D& vec2
	);

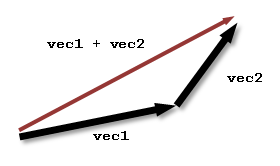
The rose_vec_sum() function does simple vector addition. The result is a vector that is equivalent to placing the two vectors head to tail. If you are combining unit direction vectors, you must call rose_vec_normalize() to normalize the result in a separate step. The rose_vec2d_sum() function is a 2D version.

double a[3] = { 1, 2, 3 }
double b[3] = { 4, 5, 6 }
double c[3];

// c = a + b  results in c = (5, 7, 9)
rose_vec_sum(c, a, b);

// c = a, followed by c += b  results in c = (5, 7, 9)
rose_vec_put(c, a);
rose_vec_sum(c, c, b);

rose_xform_apply()

void rose_xform_apply(
	double result[3],
	const double xform[16],
	const double src[3]
	);
void rose_xform_apply(
	double result[3],
	const RoseXform& xform,
	const double src[3]
	);
void rose_xform_apply(
	RosePoint& result,
	const RoseXform& xform,
	const RosePoint& src
	);
void rose_xform_apply(
	double &xout, double &yout, double &zout, 
	const RoseXform& xform,
	double xin, double yin, double zin
	);


void rose_xform2d_apply(
	double result[2],
	const double xform[9],
	const double src[2]
	);
void rose_xform2d_apply(
	double result[2],
	const RoseXform2D& xform,
	const double src[2]
	);
void rose_xform2d_apply(
	RosePoint2D& result,
	const RoseXform2D& xform,
	const RosePoint2D& src
	);
void rose_xform2d_apply(
	double &xout, double &yout,
	const RoseXform2D& xform,
	double xin, double yin
	);

The rose_xform_apply() function performs a matrix multiply to transform a location in space. This function provides class-based overloads for the RosePoint class. If you need to transform a direction vector, use the rose_xform_apply_dir() function instead.

// Make a transform that just rotates the X axis 90 degrees
// to point along Y.
RoseXform xf;
xf.xdir(0, 1, 0);
xf.ydir(-1, 0, 0);

// Transform the following point.  (1,2,3) becomes (-2,1,3)
RosePoint pt1(1, 2, 3);
RosePoint res;
rose_xform_apply(res, xf, pt1);


// Move the origin with the transform so (0,0,0) is now
// located at (10,20,30)

// Transform (1,2,3) again.  It now becomes (8, 21, 33)

xf.origin(10,20,30);
rose_xform_apply(res, xf, pt1);


// Apply the transform to a direction vector instead of a point.
// The transform still moves the origin but apply_dir() only uses
// the rotation part of the transform.	(1,2,3) becomes (-2,1,3)
//
RoseDirection dir1(1, 2, 3);
rose_xform_apply_dir(res, xf, dir1);

rose_xform_apply_dir()

void rose_xform_apply_dir(
	double result[3],
	const double xform[16],
	const double src[3]
	);
void rose_xform_apply_dir(
	double result[3],
	const RoseXform& xform,
	const double src[3]
	);
void rose_xform_apply_dir(
	RoseDirection& result,
	const RoseXform& xform,
	const RoseDirection& src
	);
void rose_xform_apply_dir(
	double &iout, double &jout, double &kout, 
	const RoseXform& xform,
	double iin, double jin, double kin
	);


void rose_xform2d_apply_dir(
	double result[2],
	const double xform[9],
	const double src[2]
	);
void rose_xform2d_apply_dir(
	double result[2],
	const RoseXform2D& xform,
	const double src[2]
	);
void rose_xform2d_apply_dir(
	RoseDirection2D& result,
	const RoseXform2D& xform,
	const RoseDirection2D& src
	);
void rose_xform2d_apply_dir(
	double &iout, double &jout,
	const RoseXform2D& xform,
	double iin, double jin
	);

The rose_xform_apply_dir() function performs a matrix multiply to rotate a direction vector to a new orientation. This function only uses the rotation part of the transform. It ignores any change of origin. There is also a class-based overload for the RoseDirection class.

Use this function fo transforming directions and rose_xform_apply() for transforming points in space. See rose_xform_apply() for examples.

rose_xform_compose()

void rose_xform_compose(
	double result[3],
	const double xf_outer[16],
	const double xf_inner[16]
	);
void rose_xform_compose(
	RoseXform& result,
	const RoseXform& xf_outer,
	const RoseXform& xf_inner
	);

void rose_xform2d_compose(
	double result[2],
	const double xf_outer[9],
	const double xf_inner[9]
	);

void rose_xform2d_compose(
	RoseXform2D& result,
	const RoseXform2D& xf_outer,
	const RoseXform2D& xf_inner
	);

The rose_xform_compose() function transforms another transformation matrix, in the same way that rose_xform_apply() transforms a point in space. The result is calculated by matrix multiplication xf_outer * xf_inner. Using a mechanical assembly as an example, inner is the local coordinate system for a bolt definition and outer is the placement of the bolt in an assembly. The rose_xform2d_compose() function is a 2D version of the function.

RoseXform xfasm;
RoseXform xfpart;
RosePoint pt1(1, 2, 3);
RosePoint res;

// coordinate system for a part.  default XYZ axis with the
// origin for the part at (10, 20, 30)
xfpart.origin(10, 20, 30);

// transform point (1,2,3) in the part.	  It will be at (11,22,33) 
rose_xform_apply(res, xfpart, pt1);


// Transform the entire part to (1000, 2000, 3000) and rotate
// 90 degrees so that the X axis points along Y.
xfasm.xdir(0, 1, 0);
xfasm.ydir(-1, 0, 0);
xfasm.origin(1000, 2000, 3000);

// transform the part point at (11,22,33) to this final coordinate
// system.  It will be at (978, 2011, 3033)
rose_xform_apply(res, xfasm, res);


// Above we applied the part tranform, then applied the assembly
// transform to the result
//
//  final =  xfasm *  (xfpart * pt1)
//
// Use compose to combine the transforms, then apply both at once
//
//  final =  (xfasm * xfpart) * pt1

RoseXform combined;
rose_xform_compose(combined, xfasm, xfpart);

// Apply both to (1,2,3) to get (978, 2011, 3033)
rose_xform_apply(res, comp, pt1);

rose_xform_compose_rotation()

void rose_xform_compose_rotation(
	double result[16],
	const double src[16],
	const double axis[3],
	const double origin[3],
	double angle,
 	RoseUnit angle_unit = roseunit_rad
	);

The rose_xform_compose_rotation() function rotates a coordinate system about an axis, angle and origin. This simply builds a rotation transform with rose_xform_put_rotation() and then composes it with the input transform.

// rotate a coordinate system 45 degrees around the Z axis
RoseXform csys;
rose_xform_compose_rotation(
    csys.m, csys.m, csys.zdir().m, csys.origin().m, 45, roseunit_deg
    );
 

// This does the same as the function.  Build rotation matrix and
// apply to the source
RoseXform rot;
rot.origin(csys.origin().m);
rot.put_rotation(csys.zdir(), 45, roseunit_deg);
rose_xform_compose(csys, rot, csys);

rose_xform_compose_scale()

void rose_xform_compose_scale(
	double result[16],
	const double xform[16],
	double scale
	);
void rose_xform_compose_scale(
	RoseXform& result,
	const RoseXform& xform,
	double scale
	);

void rose_xform_compose_scale(
	double result[16],
	const double xform[16],
	double scale_x, double scale_y, double scale_z 	// non-uniform scale
	);
void rose_xform_compose_scale(
	RoseXform& result,
	const RoseXform& xform,
	double scale_x, double scale_y, double scale_z
	);



void rose_xform2d_compose_scale(
	double result[9],
	const double xform[9],
	double scale
	);
void rose_xform2d_compose_scale(
	RoseXform2D& result,
	const RoseXform2D& xform,
	double scale
	);

void rose_xform2d_compose_scale(
	double result[9],
	const double xform[9],
	double scale_x, double scale_y	// non-uniform scale
	);
void rose_xform2d_compose_scale(
	RoseXform2D& result,
	const RoseXform2D& xform,
	double scale_x, double scale_y
	);

The rose_xform_compose_scale() function builds a transform matrix with the given scaling factors and composes it with the input matrix. The result has the scale applied to the direction components and the origin and can be useful switching between unit systems. The rose_xform2d_compose_scale() function does the same with a 2D transform.

This function is equivalent to building a scale matrix with rose_xform_scale_dirs() and then composing it with the input using rose_xform_compose()

// transform with no rotation, moves origin to (10,20,30)
RoseXform xf;
xf.origin(10,20,30);

// Add scaling to the transform so 1in goes to 25.4mm.  The origin is
// also changed to (254.0, 508.0, 762.0)
rose_xform_compose_scale(xf, xf, 25.4);

// transform point to the new space with a different origin
// and all numbers 25.4 times larger.
// (1,1,1) goes to (279.4, 533.4, 787.4)
RosePoint pt1(1,1,1);
RosePoint res;

rose_xform_apply(res, xf, pt1);

rose_xform_det()

double rose_xform_det( const double m[16] );
double rose_xform_det( const RoseXform& xf );

double rose_xform2d_det( const double xf[9] );
double rose_xform2d_det( const RoseXform2D& xf );

The rose_xform_det() function calculates the determinant of the transform as a 4x4 matrix. If the matrix array is null, the function assumes an identity matrix.

The rose_xform2d_det() function is a 2D version that finds the determinant of a double[9] array as a 3x3 matrix. This function just calls the more general rose_vec_det3x3() function. If the matrix array is null, the function assumes an identity matrix.

rose_xform_get_euler_angles()

void rose_xform_get_euler_angles(
	double * alpha, 
	double * beta, 
	double * gamma,
	const double xf[16],
 	RoseUnit angle_unit = roseunit_rad
	);
void rose_xform_get_euler_angles(
	double * alpha, 
	double * beta, 
	double * gamma,
	const RoseXform& xf,
 	RoseUnit angle_unit = roseunit_rad
	);

The rose_xform_get_euler_angles() function computes the Euler angles for the rotation portion of the matrix. The function assume the ZXZ convention: that alpha is a rotation about Z axis, followed by a beta rotation about the resulting X, followed by a gamma rotation about the resulting Z.

rose_xform_inverse()

int rose_xform_inverse(
	double result[16],
	const double xf[16]
	);
int rose_xform_inverse(
	RoseXform& result,
	const RoseXform& xf
	);

int rose_xform2d_inverse(
	double result[9],
	const double xf[9]
	);
int rose_xform2d_inverse(
	RoseXform2D& result,
	const RoseXform2D& xf
	);

The rose_xform_inverse() function computes the inverse of a general transformation matrix that might include scaling.

The function returns true if an inverse was successfully computed. If an inverse could not be found, the function returns zero and sets the result to the identity matrix.

The rose_xform2d_inverse() function is a 2D version that operates on a double[9].

RoseXform xf1, xf2, tmp;

// transforms that have some scaling
xf1.origin (12638.4, 39700.3, 20475.3);
xf1.zdir (19.113, 2.489, -16.543);
xf1.xdir (16.520, -6.767, 18.069);
rose_vec_cross(xf1.ydir(), xf1.zdir(), xf1.xdir());

xf2.origin (3.22151e-012, 16696.2, 0);
xf2.zdir (-14.569, 0.000, 20.806);
xf2.xdir (-20.806, 0.000, -14.569);
rose_vec_cross(xf2.ydir(), xf2.zdir(), xf2.xdir());

// compute the inverse of xf1, store in tmp
rose_xform_inverse(tmp, xf1);

// invert the inverse, tmp should now be equal to xf1 (within an
// epsilon)
rose_xform_inverse(tmp, tmp);

rose_xform_is_dir_identity()

int rose_xform_is_dir_identity(
	const double xf[16],
	double tol=ROSE_EPSILON
	);
int rose_xform_is_dir_identity(
	const RoseXform& xf,
	double tol=ROSE_EPSILON
	);

int rose_xform2d_is_dir_identity(
	const double xf[9],
	double tol=ROSE_EPSILON
	);
int rose_xform2d_is_dir_identity(
	const RoseXform2D& xf,
	double tol=ROSE_EPSILON
	);

The rose_xform_is_dir_identity() function returns true if the xdir, ydir and zdir part of the transform contains the identity matrix. The function only examines the rotation part of the matrix and ignores the translation part. Use rose_xform_is_identity() to examines the entire matrix.

All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use ROSE_EPSILON. The rose_xform2d_is_equal() function is a 2D version.

double bad[16] = { 99,99,99,99, 99,99,99,99, 99,99,99,99 };
double tmp[16];

double m2[16] = {
	1, 0, 0 + (ROSE_EPSILON/2.0), 0,
	0, 1, 0 + (ROSE_EPSILON/2.0), 0,
	0, 0, 1 + (ROSE_EPSILON/2.0), 0,
	20, 30, 40, 1 };

double m3[16] = {
	1, 0, 0 + (2.0*ROSE_EPSILON), 0,
	0, 1, 0 + (2.0*ROSE_EPSILON), 0,
	0, 0, 1 + (2.0*ROSE_EPSILON), 0,
	50, 60, 70, 1 };

rose_xform_put_identity(tmp);
if (rose_xform_is_dir_identity(tmp)) {
    printf(exactly ident\n);
}

if (!rose_xform_is_dir_identity(bad)) {
    printf(not ident, all vals are very different\n);
}

// NOTE that matrix m2 and m3 are NOT ZERO in the translation part!
if (rose_xform_is_dir_identity(m2)) {
    printf(identity directions, within a half-epsilon\n);
}

if (!rose_xform_is_dir_identity(m3)) {
    printf(directions NOT identity, more than an epsilon away\n);
}

if (rose_xform_is_dir_identity(m3, 3.0*ROSE_EPSILON)) {
    printf(directions now considered ident with a larger epsilon\n);
}

rose_xform_is_equal()

int rose_xform_is_equal(
	const double xf1[16],
	const double xf2[16],
	double tol=ROSE_EPSILON
	);
int rose_xform_is_equal(
	const RoseXform& xf1,
	const RoseXform& xf2,
	double tol=ROSE_EPSILON
	);

int rose_xform2d_is_equal(
	const double xf1[9],
	const double xf2[9],
	double tol=ROSE_EPSILON
	);
int rose_xform2d_is_equal(
	const RoseXform2D& xf1,
	const RoseXform2D& xf2,
	double tol=ROSE_EPSILON
	);

The rose_xform_is_equal() function returns true if each element in pair of sixteen element arrays are equal to each other. That is to say the first elements in both arrays are equal, the second elements are equal, and the so on. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use ROSE_EPSILON. The rose_xform2d_is_equal() function is a 2D version.

double bad[16] = { 99,99,99,99, 99,99,99,99, 99,99,99,99 };

double m1[16] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 };
double m2[16] = {
    1, 2, 3, 4	+ (ROSE_EPSILON/2.0),
    5, 6, 7, 8 + (ROSE_EPSILON/2.0),
    9, 10, 11, 12  + (ROSE_EPSILON/2.0),
    13, 14, 15, 16 };

double m3[16] = {
    1, 2, 3, 4	+ (2.0*ROSE_EPSILON), 
    5, 6, 7, 8 + (2.0*ROSE_EPSILON), 
    9, 10, 11, 12  + (2.0*ROSE_EPSILON), 
    13, 14, 15, 16 };

if (!rose_xform_is_equal(m1, bad )) {
    printf(not equal, vals are very different\n);
}

if (rose_xform_is_equal(m1, m2)) {
    printf(these are equal, only a half-epsilon apart\n);
}

if (!rose_xform_is_equal(m1, m3)) {
    printf(not equal, more than an epsilon apart\n);
}

if (rose_xform_is_equal(m1, m3, 3.0*ROSE_EPSILON)) {
    printf(now they are equal, because we use a larger epsilon\n);
}

rose_xform_is_identity()

int rose_xform_is_identity(
	const double xf[16],
	double tol=ROSE_EPSILON
	);
int rose_xform_is_identity(
	const RoseXform& xf,
	double tol=ROSE_EPSILON
	);

int rose_xform2d_is_identity(
	const double xf[9],
	double tol=ROSE_EPSILON
	);
int rose_xform2d_is_identity(
	const RoseXform2D& xf,
	double tol=ROSE_EPSILON
	);

The rose_xform_is_identity() function returns true if the transform contains the identity matrix, which is all zeros except elements 0, 5, 10, and 15, which are one. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use ROSE_EPSILON. The rose_xform2d_is_equal() function is a 2D version.

double bad[16] = { 99,99,99,99, 99,99,99,99, 99,99,99,99 };
double tmp[16];

double m2[16] = {
    1, 0, 0 + (ROSE_EPSILON/2.0), 0,
    0, 1, 0 + (ROSE_EPSILON/2.0), 0,
    0, 0, 1 + (ROSE_EPSILON/2.0), 0,
    0, 0, 0, 1 };

double m3[16] = {
    1, 0, 0 + (2.0*ROSE_EPSILON), 0,
    0, 1, 0 + (2.0*ROSE_EPSILON), 0,
    0, 0, 1 + (2.0*ROSE_EPSILON), 0,
    0, 0, 0, 1 };

rose_xform_put_identity(tmp);
if (rose_xform_is_identity(tmp)) {
    printf(exactly ident\n);
}

if (!rose_xform_is_identity(bad)) {
    printf(not ident, vals are very different\n);
}

if (rose_xform_is_identity(m2)) {
    printf(zero, within a half-epsilon\n);
}

if (!rose_xform_is_identity(m3)) {
    printf(not ident, more than an epsilon away\n);
}

if (rose_xform_is_identity(m3, 3.0*ROSE_EPSILON)) {
    printf(now considered ident with a larger epsilon\n);
}

rose_xform_normalize()

void rose_xform_normalize(
	double result[16],
	const double xf[16]
	);
void rose_xform_normalize(
	RoseXform& result,
	const RoseXform& xf
	);

void rose_xform2d_normalize(
	double result[9],
	const double xf[9]
	);
void rose_xform2d_normalize(
	RoseXform2D& result,
	const RoseXform2D& xf
	);

// normalize in place
void rose_xform_normalize( double result[16] );
void rose_xform_normalize( RoseXform& result );

void rose_xform2d_normalize( double result[9] );
void rose_xform2d_normalize( RoseXform2D& result );

The rose_xform_normalize() function scales the X, Y, and Z axis direction vectors that they are unit vectors (length = 1). The function calls rose_vec_normalize() on each to do the actual scaling. he rose_xform2d_normalize() function is a 2D version.

RoseXform a;
RoseXform tmp;

// put normalized version into a 
rose_xform_normalize(tmp, a);  

// replace with normalized values
rose_xform_normalize(a);

// this does the same thing
rose_vec_normalize(a.xdir()); 
rose_vec_normalize(a.ydir()); 
rose_vec_normalize(a.zdir());

rose_xform_put()

void rose_xform_put(
	double result[16], 
	const double src[16]
	);
void rose_xform_put(
	double result[16], 
	const RoseXform& xf
	);

void rose_xform2d_put(
	double result[9], 
	const double src[9]
	);
void rose_xform2d_put(
	double result[9], 
	const RoseXform2D& xf
	);

The rose_xform_put() function copies a sixteen element array of doubles. The rose_xform2d_put() function is a 2D version that copies a double[9] array and rose_vec_put() does the same thing for double[3] arrays.

When working with the RoseXform class, you can just use simple assignment with a object or array and the C++ compiler will use a copy constructor to do the right thing. The rose_xform_put() function is only needed when working with two plain arrays or copying from an object to an array.

double a[16] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 }; 
double b[16] = ROSE_XFORM_IDENTITY;

rose_xform_put(a,b);	    // a now contains identity matrix too

for (int i=0; i<16; i++) a[i]=b[i];	// same thing


// with the class wrappers, C++ handles the copy
RoseXform xf;

xf = a;	   // a now contains 1,2,3,4 etc

// copy back to an array requires the function, though
rose_xform_put(b,xf.m);

rose_xform_put_alldirs()

void rose_xform_put_alldirs(
	double result[16],
	const double src[16]
	);
void rose_xform_put_alldirs(
	double result[16],
	const double xdir[3],
	const double ydir[3],
	const double zdir[3]
	);

void rose_xform2d_put_alldirs(
	double result[9],
	const double src[9]
	);
void rose_xform2d_put_alldirs(
	double result[9],
	const double xdir[2],
	const double ydir[2]
	);

The rose_xform_put_alldirs() function copies all of the direction vector portions of a sixteen element array, which is the first 12 elements. This function takes a full transform array, or three separate direction arrays. When working with the RoseXform class, use the put_alldirs() member function.

The rose_xform2d_put_alldirs() function is a 2D version that operates on a nine element array. The three examples below show equivalent code.

The rose_xform_put_dirs() function is more appropriate if you need to initialize a transform, only have Z and X axis directions, and need to normalize and compute the Y axis. This is common with STEP and IFC axis2_placement3d objects.

double a[16] = { some initializer };
double b[16] = { some initializer };

rose_xform_put_alldirs(a,b);	  

rose_xform_put_alldirs(
	a, ROSE_XFORM_XDIR(b), ROSE_XFORM_YDIR(b), ROSE_XFORM_ZDIR(b)
	); 


// copy manually, be sure to get the array index right!
// NOTE the functions also initialize a[3], a[7], and a[11]
//
a[0]=b[0];	or ROSE_XFORM_XDIR(a)[0]=ROSE_XFORM_XDIR(b)[0];
a[1]=b[1];	or ROSE_XFORM_XDIR(a)[1]=ROSE_XFORM_XDIR(b)[1];
a[2]=b[2];	or ROSE_XFORM_XDIR(a)[2]=ROSE_XFORM_XDIR(b)[2];

a[4]=b[4];	or ROSE_XFORM_YDIR(a)[0]=ROSE_XFORM_YDIR(b)[0];
a[5]=b[5];	or ROSE_XFORM_YDIR(a)[1]=ROSE_XFORM_YDIR(b)[1];
a[6]=b[6];	or ROSE_XFORM_YDIR(a)[2]=ROSE_XFORM_YDIR(b)[2];

a[8]=b[8];	or ROSE_XFORM_ZDIR(a)[0]=ROSE_XFORM_ZDIR(b)[0];
a[9]=b[9];	or ROSE_XFORM_ZDIR(a)[1]=ROSE_XFORM_ZDIR(b)[1];
a[10]=b[10];	or ROSE_XFORM_ZDIR(a)[2]=ROSE_XFORM_ZDIR(b)[2];

rose_xform_put_cto()

void rose_xform_put_cto(
	double xform[16],
	const double xd[3],
	const double yd[3],
	const double zd[3],
	const double loc[3],
	double scale = 1.0
	);

void rose_xform2d_put_cto(
	double xform[9],
	const double xd[2],
	const double yd[2],
	const double loc[2],
	double scale = 1.0
	);

The rose_xform_put_cto() function constructs an array from a cartesian transform operator, which is a generalized transform that can do rotation, translation, uniform scaling, and mirroring (by giving a left handed set of direction vectors). When working with the RoseXform class, use the put_cto() member function.

The function expects direction vectors for the X-axis, Y-axis, Z-axis, a location vector, and an optional scale factor. Any of the vectors can be null or zero vectors. As with rose_xform_put_dirs(), This function follows the STEP and IFC Part 42 EXPRESS logic for building the axes when they are missing.

The rose_xform2d_put_cto() function is a 2D version that takes an X and Y axis directions along with position and scale.

rose_xform_put_dirs()

void rose_xform_put_dirs(
	double result[16],
	const double zdir[3],
	const double xdir[3]
	);

void rose_xform2d_put_dirs(
	double result[9],
	const double xdir[2]
	);

The rose_xform_put_dirs() function takes Z and X axis directions, computes a Y axis direction, makes sure that the resulting three axis directions are normalized and orthogonal, and stores the values in the first 12 elements of a transform matrix array. You can completely initialize a transfrorm by calling this function followed by rose_xform_put_origin(). When working with the RoseXform class, use the put_dirs() member function.

This way of describing a rotation transform is used by STEP and IFC axis2_placement3d objects and the function will handle null pointers or zero vectors (0,0,0) by choosing the appropriate defaults.

The rose_xform2d_put_dirs() function is a 2D version that takes an X axis direction, computes a Y axis direction, makes sure the results are normalized, and stores the values in the first 6 elements of a 2D transform matrix array.

double xf[16];
double minux_xaxis = { -1, 0, 0 };
double zaxis = { 0, 0, 1 };

// Set rotation to 180deg counterclockwise about the Z axis.
// The Y direction will be (0, -1, 0)	Finish by setting the
// translation portion to (10, 20, 30)

rose_xform_put_dirs(xf, zaxis, minux_xaxis);	  
rose_xform_put_origin(xf, 10, 20, 30);	    

// Same thing with axis vectors that are not normalized.   The 
// final result will have X, Y, and Z directions scaled to unit
// vectors, so you will get the same matrix as above.

double xf2[16];
double denorm_minux_xaxis = { -50, 0, 0 };
double denorm_zaxis = { 0, 0, 234 };

rose_xform_put_dirs(xf2, denorm_zaxis, denorm_minux_xaxis);	 
rose_xform_put_origin(xf2, 10, 20, 30);	     


if (rose_xform_is_equal(xf, xf2))
   printf(See! Same result!\n);

rose_xform_put_euler_angles()

void rose_xform_put_euler_angles(
	double result[16],
	double alpha, 
	double beta, 
	double gamma,
 	RoseUnit angle_unit = roseunit_rad
	);
void rose_xform_put_euler_angles(
	RoseXform& xf,
	double alpha, 
	double beta, 
	double gamma,
	RoseUnit angle_unit = roseunit_rad
	);

The rose_xform_put_euler_angles() function replaces the rotation part of the matrix with a transform that rotates by a the given Euler angles. You must compose the result if you want to rotate an existing coordinate system by that amount.

The function assume the ZXZ convention: that alpha is a rotation about Z axis, followed by a beta rotation about the resulting X, followed by a gamma rotation about the resulting Z.

rose_xform_put_frustrum()

void rose_xform_put_frustrum(
	double result[16],
	double left,
	double right,
	double bottom,
	double top,
	double nearVal,
	double farVal
	);
void rose_xform_put_frustrum(
	RoseXform& xf,
	double left,
	double right,
	double bottom,
	double top,
	double nearVal,
	double farVal
	);

The rose_xform_put_frustrum() function initializes the matrix to a perspective projection for the given square frustrum. The arguments follow the pattern originally established by the glFrustrum() function.

The left and right arguments specify the coordinates for the left and right vertical clipping planes. The bottom and top arguments specify the coordinates for the bottom and top horizontal clipping planes. And the nearVal and farVal specify the distances to the near and far depth clipping planes. Both of these distances must be positive.

rose_xform_put_identity()

void rose_xform_put_identity  ( double result[16] );
void rose_xform2d_put_identity( double result[9] );

The rose_xform_put_identity() function initializes all elements of a sixteen element array with an identity matrix. Each direction portions will point along its customary axis and the origin will be at all zeros. The rose_xform2d_put_identity() function is a 2D version that initializes a nine element array. You can also use the ROSE_XFORM_IDENTITY macro to initialize an array variable.

When working with RoseXform, you should just call the put_identity() member function.

double a[16];

// b initialized to an identity matrix
double b[16] = { 1, 0, 0, 0,   0, 1, 0, 0,   0, 0, 1, 0,   0, 0, 0, 1 };

// c initialized to same thing via macro
double c[16] = ROSE_XFORM_IDENTITY;

// set to identity matrix by function
rose_xform_put_identity(a);	  

// the hard way, set everything to zero, then set diagonal to 1
for (int i=0; i<16; i++) a[i]=0;
a[0]=a[5]=a[10]=a[15]=1;

// with the classes, the default ctor initializes to identity matrix
RoseXform xf;

// set to identity matrix again
xf.put_identity();

rose_xform_put_origin()

void rose_xform_put_origin(
	double result[16],
	const double pt[3]
	);
void rose_xform_put_origin(
	double result[16],
	double x, double y, double z
	);
void rose_xform_put_origin(
	double result[16],
	ListOfDouble * lst
	);
void rose_xform_put_origin(
	double result[16],
	const RosePoint& pt
	);


void rose_xform2d_put_origin(
	double result[9],
	const double pt[2]
	);
void rose_xform2d_put_origin(
	double result[9],
	double x, double y
	);
void rose_xform2d_put_origin(
	double result[9],
	ListOfDouble * lst
	);
void rose_xform2d_put_origin(
	double result[9],
	const RosePoint2D& pt
	);

The rose_xform_put_origin() function copies a set of three coordinates (x, y, z) to the origin portion of a sixteen element array. The function takes an array of three values, three separate arguments, or a list object. The rose_xform2d_put_origin() function is a 2D version that works on a double[9] array.

Use rose_xform_put_xdir(), rose_xform_put_ydir(), or rose_xform_put_zdir() to set the axis directions in the array.

double a[16] = { initialized to some values };
double b[16] = { initialized to some values };

// a position in space
double pt[3] = { 100, 100, 0 };

// then copy position from array
rose_xform_put_origin(a, pt); 

// set position directly from arguments
rose_xform_put_origin(a, 100, 100, 0);

// copy position from b transform to a 
rose_xform_put_origin(a, ROSE_XFORM_ORIGIN(b));

// copy manually
a[12]=pt[0];	or ROSE_XFORM_ORIGIN(a)[0]=pt[0];
a[13]=pt[1];	or ROSE_XFORM_ORIGIN(a)[1]=pt[1];
a[14]=pt[2];	or ROSE_XFORM_ORIGIN(a)[2]=pt[2];

rose_xform_put_ortho()

void rose_xform_put_ortho(
	double result[16],
	double left,
	double right,
	double bottom,
	double top,
	double nearVal,
	double farVal
	);
void rose_xform_put_ortho(
	RoseXform& xf,
	double left,
	double right,
	double bottom,
	double top,
	double nearVal,
	double farVal
	);

The rose_xform_put_ortho() function initializes the matrix to an orthographic projection for the given clipping planes. The arguments follow the pattern originally established by the glOrtho() function.

rose_xform_put_rotation()

void rose_xform_put_rotation(
	double result[16],
	const double axis[3],
	double angle,
 	RoseUnit angle_unit = roseunit_rad
	);

void rose_xform2d_put_rotation(
	double result[9],
	double angle,
 	RoseUnit angle_unit = roseunit_rad
	);

The rose_xform_put_rotation() function sets the rotation part of the matrix with a transform that rotates by a certain angle along the given axis. The origin portion is not initialized or touched. See rose_xform_put_rotation_about_pt for a complete matrix that rotates about an axis and point. Use rose_xform_compose_rotation() if you want to rotate an existing matrix by some angle.

The direction of rotation is given by the right-hand rule with your thumb aligned along the given axis. By default, the angle is expected in radians, but you can use degrees by giving an extra unit parameter. When working with the RoseXform class, use the put_rotation() member function.

The 2D version does not need an axis because it just describes a rotation in the XY plane. The RoseXform2D class also has a put_rotation() member function.

double rot[16] = { initialized to some values };
double axis[3] = { 0, 0, 1 };

double src[3] = { 1, 0, 0 };
double dst[3];

// rotate 90deg counterclockwise around the Z axis
rose_xform_put_rotation (rot, axis, 90, roseunit_deg);

// apply to a src vec that points along X
rose_xform_apply_dir (dst, rot, src);

// dst vec now points along Y (0, 1, 0)

rose_xform_put_rotation_about_pt()

void rose_xform_put_rotation_about_pt(
	double result[16],
	const double axis[3],
	const double pt[3],
	double angle,
 	RoseUnit angle_unit = roseunit_rad
	);

void rose_xform2d_put_rotation_about_pt(
	double result[9],
	const double pt[2],
	double angle,
 	RoseUnit angle_unit = roseunit_rad
	);

The rose_xform_put_rotation_about_pt() function creates a complete transformation matrix for rotating about a given point and axis. The RoseXform class, use the put_rotation_about_pt() member function.

The 2D version does not need an axis because it just describes a rotation in the XY plane. The RoseXform2D class also has a put_rotation_about_pt() member function.

rose_xform_put_xdir()

void rose_xform_put_xdir(
	double result[16],
	const double xdir[3]
	);
void rose_xform_put_xdir(
	double result[16],
	double i, double j, double k
	);
void rose_xform_put_xdir(
	double result[16],
	ListOfDouble * lst
	);
void rose_xform_put_xdir(
	double result[16],
	const RoseDirection& dir
	);


void rose_xform2d_put_xdir(
	double result[9],
	const double xdir[2]
	);
void rose_xform2d_put_xdir(
	double result[9],
	double i, double j
	);
void rose_xform2d_put_xdir(
	double result[9],
	ListOfDouble * lst
	);
void rose_xform2d_put_xdir(
	double result[9],
	const RoseDirection2D& dir
	);

The rose_xform_put_xdir() function copies a set of three direction components (i, j, k) to the X-axis portion of a sixteen element array. The function take an array of three values, three separate numbers, or a list object. The rose_xform2d_put_xdir() function is a 2D version for a double[9] array.

Use rose_xform_put_ydir() to set the Y-axis direction and rose_xform_put_zdir() to set the Z-axis direction. Call rose_xform_put_origin() to set the coordinates of the origin.

The array contains a fourth element for each direction (the transform is a 4x4 matrix) which is set by these functions. Calling the "put" functions for xdir, ydir, zdir, and origin will completely initialize a transform array.

double a[16] = { initialized to some values };
double b[16] = { initialized to some values };

// a direction at 45 degrees in the XY plane
double dir[3] = { 1/ROSE_SQRT_2, 1/ROSE_SQRT_2, 0 }

// then copy dir into the x direction
rose_xform_put_xdir(a, dir); 

// set x direction directly from arguments
rose_xform_put_xdir(a, 1/ROSE_SQRT_2, 1/ROSE_SQRT_2, 0 ); 

// copy x direction from b transform to a 
rose_xform_put_xdir(a, ROSE_XFORM_XDIR(b));

// Initialize to a 90-degree rotation about Y-axis
rose_xform_put_xdir(a, 0, 0, -1);
rose_xform_put_ydir(a, 0, 1, 0);
rose_xform_put_zdir(a, 1, 0, 0);
rose_xform_put_origin(a, 0, 0, 0);


// copy manually, be sure to get the array index right
// if you are setting the y or z directions!   And  set
// the fourth element to zero if not already initialized.
//
a[0]=dir[0];	or ROSE_XFORM_XDIR(a)[0]=dir[0];
a[1]=dir[1];	or ROSE_XFORM_XDIR(a)[1]=dir[1];
a[2]=dir[2];	or ROSE_XFORM_XDIR(a)[2]=dir[2];

rose_xform_put_ydir()

void rose_xform_put_ydir(
	double result[16],
	const double ydir[3]
	);
void rose_xform_put_ydir(
	double result[16],
	double i, double j, double k
	);
void rose_xform_put_ydir(
	double result[16],
	ListOfDouble * lst
	);
void rose_xform_put_ydir(
	double result[16],
	const RoseDirection& dir
	);


void rose_xform2d_put_ydir(
	double result[9],
	const double ydir[2]
	);
void rose_xform2d_put_ydir(
	double result[9],
	double i, double j
	);
void rose_xform2d_put_ydir(
	double result[9],
	ListOfDouble * lst
	);
void rose_xform2d_put_ydir(
	double result[9],
	const RoseDirection2D& dir
	);

The rose_xform_put_ydir() function copies a set of three direction components (i, j, k) to the Y-axis portion of a sixteen element array. The function takes an array of three values, three separate numbers, or a list object. The rose_xform2d_put_ydir() function is a 2D version that works on a double[9] array.

See rose_xform_put_xdir() for some examples.

rose_xform_put_zdir()

void rose_xform_put_zdir(
	double result[16],
	const double zdir[3]
	);
void rose_xform_put_zdir(
	double result[16],
	double i, double j, double k
	);
void rose_xform_put_zdir(
	double result[16],
	ListOfDouble * lst
	);
void rose_xform_put_zdir(
	double result[16],
	const RoseDirection& dir
	);

The rose_xform_put_zdir() function copies a set of three direction components (i, j, k) to the Z-axis portion of a sixteen element array. The function takes an array of three values, three separate numbers, or a list object.

See rose_xform_put_xdir() for some examples.

rose_xform_scale_dirs()

void rose_xform_scale_dirs(
	double result[16],
	const double xform[16],
	double scale
	);
void rose_xform_scale_dirs(
	RoseXform& result,
	const RoseXform& xform,
	double scale
	);

void rose_xform_scale_dirs(
	double result[16],
	const double xform[16],
	double scale_x, double scale_y, double scale_z 	// non-uniform scale
	);
void rose_xform_scale_dirs(
	RoseXform& result,
	const RoseXform& xform,
	double scale_x, double scale_y, double scale_z
	);



void rose_xform2d_scale_dirs(
	double result[9],
	const double xform[9],
	double scale
	);
void rose_xform2d_scale_dirs(
	RoseXform2D& result,
	const RoseXform2D& xform,
	double scale
	);

void rose_xform2d_scale_dirs(
	double result[9],
	const double xform[9],
	double scale_x, double scale_y	// non-uniform scale
	);
void rose_xform2d_scale_dirs(
	RoseXform2D& result,
	const RoseXform2D& xform,
	double scale_x, double scale_y
	);

The rose_xform_scale_dirs() functions apply a scaling factor to the directions of a transform. The origin is not changed. The scaling factor can be different for each direction or the same for all. Multiple calls are cumulative — two calls with a scale of 2.0 results in a scale of 4.0. Call rose_xform_normalize to remove any scaling.

Use rose_xform_compose_scale() to apply a scaling factor to an axis placement, including the origin, for transforming placements between different unit systems.

The rose_xform2d_scale_dirs() function applies scaling to the directions of a 2D transform, either uniformly or with separate scales for the X and Y directions.

// transform with no rotation, moves origin to (10,20,30)
RoseXform xf;
rose_xform_scale_dirs(xf, xf, 2.0);
rose_xform_scale_dirs(xf, xf, 2.0);
// scaling is now 4.0

rose_xform_normalize(xf);
// scaling is now 1.0

rose_xform_scale_dirs(xf, xf, 2.0);
// scaling is now 4.0

rose_xform_transform_to()

int rose_xform_transform_to(
        double result[16], 
        const double src[16], 
        const double dst[16]
        );
int rose_xform_transform_to(
        RoseXform& result,
        const RoseXform& src,
        const RoseXform& dst
        );

int rose_xform2d_transform_to(
        double result[9], 
        const double src[9], 
        const double dst[9]
        );
int rose_xform2d_transform_to(
        RoseXform2D& result,
        const RoseXform2D& src,
        const RoseXform2D& dst
        );

The rose_xform_transform_to() function creates a transform that will move items in the source coordinate system to the destination system. It does this by inverting the source matrix and then composing it with the destination one. The fuction returns nonzero if it succeeds and zero if it fails to compute the inverse, as discussed by rose_xform_inverse()

double src[16], dst[16], src2dst[16];

rose_xform_transform_to(src2dst, src, dst);

// equivalent code 
double tmp[16];

/* transform to origin, then to dst */
if (!rose_xform_inverse(tmp, src))
    return 0;

rose_xform_compose(src2dst, dst, tmp);
return 1;

rose_xform_translate()

void rose_xform_translate(
	double result[16],
	const double xf[16],
	double x,
	double y,
	double z
	);
void rose_xform_translate(
        RoseXform& result,
        const RoseXform& xf,
	double x,
	double y,
	double z
	);

void rose_xform2d_translate(
	double result[9],
	const double xf[9],
	double x,
	double y
	);
void rose_xform2d_translate(
        RoseXform2D& result,
        const RoseXform2D& xf,
	double x,
	double y
	);

The rose_xform_translate() function moves the origin of the transform matrix by the given distances along the directions given by the transform for the X, Y, and Z axes. The rose_xform2d_translate() function moves the origin of a 2D transform matrix by the given distances along the directions given by the transform for the X and Y axes.

rose_xform_transpose()

void rose_xform_transpose(
	double result[16],
	const double xf[16]
	);
void rose_xform_transpose(
        RoseXform& result,
        const RoseXform& xf
	);


void rose_xform2d_transpose(
	double result[9],
	const double xf[9]
	);
void rose_xform2d_transpose(
        RoseXform2D& result,
        const RoseXform2D& xf
        );

The rose_xform_transpose() function transposes the 4x4 matrix of the transform, making columns into rows and rows into columns. The rose_xform2d_transpose() does the same with the 3x3 matrix of the 2D transform.