Overview
Engineering data describes direction vectors, points in space, and
transformation matrices. The Vec and Xform
APIs have functions to work with these concepts and application code
can build upon them for things specific to STEP geometry.
The functions use lists of floats because that is the simplest and most widely applicable form. Points and direction vectors are a list of three floats while transforms are a list of sixteen floats
The transforms follow the GL usage shown below.
# xf[0-2] is the x axis direction, xf[3] is zero # xf[4-6] is the y axis direction, xf[7] is zero # xf[8-10] is the z axis direction, xf[11] is zero # xf[12-14] is the origin, xf[15] is one XF = [ xi, xj, xk, 0.0, yi, yj, yk, 0.0, zi, zj, zk, 0.0, wx, wy, wz, 1.0 ] # use sublists to get the components of a transform XDIR = XF[0:3] YDIR = XF[4:7] ZDIR = XF[8:11] ORIGIN = XF[12:15]
Be aware that math books, wikipedia, and even GL manuals show the values as a 4x4 matrix in column order (xdir is the first column, ydir is the second column, etc). This is the correct mathematical notation, but can be confusing if you have a mental picture of the list as four rows. Just use the roadmap above and everything will be fine.
Vec.cross()
@classmethod def cross(self, v1: Sequence[float], v2: Sequence[float] ) -> List[float]:
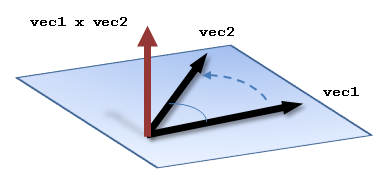
The Vec.cross() function calculates the cross product of two 3D vectors (v1 x v2) and returns the result. The cross product produces a vector perpendicular to the plane formed by the two input vectors, with the direction given by the right hand rule
XAXIS = [1, 0, 0];
YAXIS = [0, 1, 0];
print (step.Vec.cross(XAXIS, YAXIS))
==> [0.0, 0.0, 1.0]
Vec.diff()
@classmethod def diff(self, v1: Sequence[float], v2: Sequence[float] ) -> List[float]:
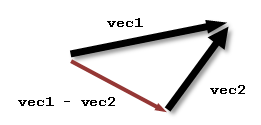
The Vec.diff() function does simple vector subtraction. The result is a vector that is equivalent to v1 minus the v2. If you are combining unit direction vectors, you must call Vec.normalize() to normalize the result in a separate step.
A = [ 40, 50, 60 ]
B = [ 1, 2, 3 ]
print(Vec.diff(A, B))
==> [39.0, 48.0, 57.0]
Vec.dot()
@classmethod def dot(self, v1: Sequence[float], v2: Sequence[float] ) -> float:
The Vec.dot() function calculates the dot product of two 3D vectors (v1 ⋅ v2). The dot product is the length of the projection of the first vector upon the second, which is can be found by multiplying the length of the first vector by the cosine of the angle between them.
Vec.is_equal()
@classmethod def is_equal(self, v1: Sequence[float], v2: Sequence[float], epsilon: float = None ) -> bool:
The Vec.is_equal() function returns true if each element in pair of three element lists are equal to each other. That is to say the first elements in both lists are equal, the second elements are equal, and the third elements are equal. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use a default.
# very different step.Vec.is_equal([1,2,3], [4,5,6]) ==> False # half epsilon step.Vec.is_equal([1,2,3], [1,2,3+0.05], 0.1) ==> True # twice epsilon step.Vec.is_equal([1,2,3], [1,2,3+0.2], 0.1) ==> False
Vec.is_zero()
@classmethod def is_zero(self, v1: Sequence[float], epsilon: float = None ) -> bool:
The Vec.is_zero() function returns true if each element in a three element array is zero. All comparisons are done with epsilon value that you can provide. If you do not provide one, the function will use a default. This function is equivalent to calling Vec.is_equal() to compare with (0,0,0).
# exactly zero step.Vec.is_zero([0,0,0]) ==> True # not zero step.Vec.is_zero([4,5,6]) ==> False # half epsilon step.Vec.is_zero([0,0,0.05], 0.1) ==> True # twice epsilon step.Vec.is_zero([0,0,0.2], 0.1) ==> False
Vec.length()
@classmethod def length(self, v1: Sequence[float] ) -> float:
The Vec.length() function returns the length, also called
the magnitude, of a 3D vector. In versions of Python newer than 3.8,
the math.hypot() function can also be used to find this
value.
A = [0.0, 0.0, 5.0] print (Length: %.2f% step.Vec.length(A)) ==> Length: 5.00 A = [30/math.sqrt(3),30/math.sqrt(3),30/math.sqrt(3)] print (TEST VEC: %.2f, %.2f, %.2f% tuple(A)) print (Length: %.2f% step.Vec.length(A)) print (Hypot: %.2f% math.hypot(*A)) TEST VEC: 17.32, 17.32, 17.32 ==> Length: 30.00 ==> Hypot: 30.00
Vec.negate()
@classmethod def negate(self, v1: Sequence[float] ) -> List[float]:
The Vec.negate() function reverses the i,j,k components of a vector so that it points in the opposite direction. The returned vector is -i,-j,-k.
step.Vec.negate([10, 20, 30])
==> [-10.0, -20.0, -30.0]
Vec.normalize()
@classmethod def normalize(cls, v1: Sequence[float] ) -> List[float]:
The Vec.normalize() function scales the i,j,k components of a vector so that it is a unit vector (length = 1) and returns the result. If the length is smaller than an epsilon, all components will be zeros.
step.Vec.negate([0, 0, 90])
==> [0.0, 0.0, 1.0]
Vec.scale()
@classmethod def scale(self, v1: Sequence[float], scale: float ) -> List[float]:
The Vec.scale() function multiplies a scalar constant C to the i,j,k components of a vector. The new vector is C*i,C*j,C*k.
# scale by five step.Vec.scale([10, 20, 30], 5) ==> [50.0, 100.0, 150.0]
Vec.sum()
@classmethod def sum(self, v1: Sequence[float], v2: Sequence[float] ) -> List[float]:
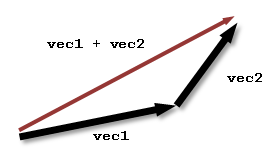
The Vec.sum() function does simple vector addition. The result is a vector that is equivalent to placing the two vectors head to tail. If you are combining unit direction vectors, you must call Vec.normalize() to normalize the result in a separate step.
# c = a + b results in c = (5, 7, 9) step.Vec.sum([1,2,3],[4,5,6]) ==> [5.0, 7.0, 9.0]
Xform.apply()
@classmethod def apply(self, xf: Sequence[float], pnt: Sequence[float] ) -> List[float]:
The Xform.apply() function performs a matrix multiply to transform a location in space and returns the resulting point. Use the Xform.apply_dir() if you need to transform a direction vector.
# Make a transform that just rotates the X axis 90 degrees. # to point along Y. XF = [ 0, 1, 0, 0, -1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 ] # Transform the following point. (1,2,3) becomes (-2,1,3) print(step.Xform.apply(XF, [1, 2, 3])) ==> [-2.0, 1.0, 3.0] # Keep the same direction transform but move the origin # so (0,0,0) is now located at (10,20,30) XF = [ 0, 1, 0, 0, -1, 0, 0, 0, 0, 0, 1, 0, 10, 20, 30, 1 ] Transform (1,2,3) again. It now becomes (8, 21, 33) print(step.Xform.apply(XF, [1, 2, 3])) ==> [8.0, 21.0, 33.0] # Apply only the axis rotation part of the transform. # Here (1,2,3) becomes (-2,1,3) as before when the transform # did not have any translation. print(step.Xform.apply_dir(XF, [1, 2, 3])) ==> [-2.0, 1.0, 3.0]
Xform.apply_dir()
@classmethod def apply_dir(self, xf: Sequence[float], dir: Sequence[float] ) -> List[float]:
The Xform.apply_dir() function performs a matrix multiply to rotate a direction vector to a new orientation. This function only uses the rotation part of the transform and ignores any change of origin. See Xform.apply() for an example.
Xform.compose()
@classmethod def compose(self, outer_xf: Sequence[float], inner_xf: Sequence[float] ) -> List[float]:
The Xform.compose() function transforms another transformation matrix, in the same way that Xform.apply() transforms a point in space. The result is calculated by matrix multiplication xf_outer * xf_inner. Using a mechanical assembly as an example, inner is the local coordinate system for a bolt definition and outer is the placement of the bolt in an assembly.
# coordinate system for a part. default XYZ axis with the # origin for the part at (10, 20, 30) XFPART = [ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 10, 20, 30, 1 ] # transform point (1,2,3) in the part. It will be at (11,22,33) print(step.Xform.apply(XFPART, [1,2,3])) ==> [11.0, 22.0, 33.0] # Transform the entire part to (1000, 2000, 3000) and rotate # 90 degrees so that the X axis points along Y. XFASM = [ 0, 1, 0, 0, -1, 0, 0, 0, 0, 0, 1, 0, 1000, 2000, 3000, 1 ] # transform the part point at (11,22,33) to this final coordinate # system. It will be at (978, 2011, 3033) print(step.Xform.apply(XFASM, [11,22,33])) ==> [978.0, 2011.0, 3033.0] # Above we applied the part tranform, then applied the assembly # transform to the result # # final = xfasm * (xfpart * pt1) # # Use compose to combine the transforms, then apply both at once # # final = (xfasm * xfpart) * pt1 COMBINED = step.Xform.compose(XFASM, XFPART) # Apply both to (1,2,3) to get (978, 2011, 3033) print(step.Xform.apply(COMBINED, [1,2,3])) ==> [978.0, 2011.0, 3033.0]
Xform.compose_rotation()
@classmethod def compose_rotation(self, xf: Sequence[float], axis: Sequence[float], origin: Sequence[float], angle: float, angle_unit: Unit = Unit.RAD ) -> List[float]:
The Xform.compose_rotation() function rotates a coordinate system about an axis, angle and origin. This simply builds a rotation transform and then composes it with the input transform.
XF = step.Xform.identity() # Starting with identity matrix, rotate 90deg around Z # This moves XF = step.Xform.compose_rotation(XF, [0,0,1], [0,0,0], 90, step.Unit.DEG) print ((90deg around Z\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(XF)) ==> 90deg around Z: [0.00, 1.00, 0.00, 0.00, -1.00, 0.00, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00, 0.00, 0.00, 0.00, 1.00] # Now rotate that 90deg around X XF = step.Xform.compose_rotation(XF, [1,0,0], [0,0,0], 90, step.Unit.DEG) print ((90deg around X\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(XF)) ==> 90deg around X [0.00, 0.00, 1.00, 0.00, -1.00, 0.00, 0.00, 0.00, 0.00, -1.00, 0.00, 0.00, 0.00, 0.00, 0.00, 1.00]
Xform.compose_scale()
@classmethod def compose_scale(self, xf: Sequence[float], scale: float ) -> List[float]:
The Xform.compose_scale() function builds a transform matrix with the given scaling factors and composes it with the input matrix. The result has the scale applied to the direction components and the origin and can be useful switching between unit systems.
XF = [ 1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
10, 20, 30, 1 ]
# Add scaling to the transform so 1in goes to 25.4mm. The
# origin is also changed to (254.0, 508.0, 762.0)
XF = step.Xform.compose_scale(XF, 25.4)
print ((Inch to MM\n
+
[%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f]
) % tuple(XF))
==> Inch to MM
[25.40, 0.00, 0.00, 0.00,
0.00, 25.40, 0.00, 0.00,
0.00, 0.00, 25.40, 0.00,
254.00, 508.00, 762.00, 1.00]
# transform point to the new space with a different origin
# and all numbers 25.4 times larger.
# (1,1,1) goes to (279.4, 533.4, 787.4)
print (step.Xform.apply(XF, [1,1,1]))
==> [279.4, 533.4, 787.4]
Xform.det()
@classmethod def det(self, xf: Sequence[float] ) -> float:
The Xform.det() function calculates the determinant of the transform as a 4x4 matrix.
Xform.get_euler_angles()
@classmethod def get_euler_angles(self, xf: Sequence[float], angle_unit: Unit = Unit.RAD ) -> Tuple[float,float,float]
The Xform.get_euler_angles() function computes the Euler angles for the rotation portion of the matrix. The function assume the ZXZ convention: that alpha is a rotation about Z axis, followed by a beta rotation about the resulting X, followed by a gamma rotation about the resulting Z. The function returns a tuple containing the alpha, beta, and gamma angles in either radians or degrees.
XF = step.Xform.identity() ALPHA = 45 BETA = 20 GAMMA = 25 # rotate in Z first, then X, then Z. Use sublists to get the # origin and X/Z directions from the transform XF = step.Xform.compose_rotation(XF, XF[8:11], XF[12:15], ALPHA, step.Unit.DEG) XF = step.Xform.compose_rotation(XF, XF[0:3], XF[12:15], BETA, step.Unit.DEG) XF = step.Xform.compose_rotation(XF, XF[8:11], XF[12:15], GAMMA, step.Unit.DEG) print ((ZXZ Rotations\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(XF)) ==> ZXZ Rotations [0.36, 0.92, 0.14, 0.00, -0.90, 0.30, 0.31, 0.00, 0.24, -0.24, 0.94, 0.00, 0.00, 0.00, 0.00, 1.00] ANGS = step.Xform.get_euler_angles(XF, step.Unit.DEG) print (Euler angles: %.2f, %.2f, %.2f% ANGS) ==> Euler angles: 45.00, 20.00, 25.00
Xform.identity()
@classmethod def identity(self) -> List[float]:
The Xform.identity() function returns a sixteen element list containing the identity matrix.
A = step.Xform.identity() print ((Identity\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(A)) ==> Identity [1.00, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00, 0.00, 0.00, 0.00, 1.00]
Xform.inverse()
@classmethod def inverse(self, xf: Sequence[float] ) -> List[float]:
The Xform.inverse() function computes and returns the inverse of a general transformation matrix that might include scaling. If an inverse could not be found, the function raises a value exception.
XF = [ 4, 0, 0, 0,
0, 2, 0, 0,
0, 0, 3, 0,
1, 2, 3, 1 ]
TMP = step.Xform.inverse(XF)
print ((Inverse:\n
+
[%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f]
) % tuple(TMP))
==> Inverse:
[0.25, 0.00, 0.00, 0.00,
0.00, 0.50, 0.00, 0.00,
0.00, 0.00, 0.33, 0.00,
-0.25, -1.00, -1.00, 1.00]
Xform.is_dir_identity()
@classmethod def is_dir_identity(self, xf: Sequence[float], epsilon: float = None ) -> bool:
The Xform.is_dir_identity() function returns true if the xdir, ydir and zdir part of the transform contains the identity matrix. The function only examines the rotation part of the matrix and ignores the translation part. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use a default.
Use Xform.is_identity() to examines the entire matrix.
Xform.is_equal()
@classmethod def is_equal(self, xf1: Sequence[float], xf2: Sequence[float], epsilon: float = None ) -> bool:
The Xform.is_equal() function returns true if each element in a pair of sixteen element lists are equal to each other. That is to say the first elements in both arrays are equal, the second elements are equal, and the so on. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use a default.
XF = [ 1, 2, 3, 4,
5, 6, 7, 8,
9, 10, 11, 12,
13, 14, 15, 16 ]
print (very different:
, step.Xform.is_equal(XF, step.Xform.identity()))
==> very different: False
TMP = [ 1, 2, 3, 4 + 0.05,
5, 6, 7, 8 + 0.05,
9, 10, 11, 12 + 0.05,
13, 14, 15, 16 ]
print (half epsilon:
, step.Xform.is_equal(XF,TMP, 0.1))
==> half epsilon: True
TMP = [ 1, 2, 3, 4 + 0.2,
5, 6, 7, 8 + 0.2,
9, 10, 11, 12 + 0.2,
13, 14, 15, 16 ]
print (twice epsilon:
, step.Xform.is_equal(XF,TMP, 0.1))
==> twice epsilon: False
print (larger epsilon:
, step.Xform.is_equal(XF,TMP, 0.3))
==> larger epsilon: True
Xform.is_identity()
@classmethod def is_identity(self, xf: Sequence[float], epsilon: float = None ) -> bool:
The Xform.is_identity() function returns true if the transform contains the identity matrix, which is all zeros except elements 0, 5, 10, and 15, which are one. All comparisons are done with an epsilon value that you can provide. If you do not provide one, the function will use a default.
Xform.normalize()
@classmethod def normalize(self, xf: Sequence[float] ) -> List[float]:
The Xform.normalize() function scales the X, Y, and Z axis direction vectors that they are unit vectors (length = 1). The function calls Vec.normalize() on each to do the actual scaling.
XF = [ -1*567, 0, 0, 0,
0, -1*23, 0, 0,
0, 0, 1*0.0001, 0,
1, 2, 3, 1 ]
XF = step.Xform.normalize(XF)
print ((Normalize:\n
+
[%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f]
) % tuple(XF))
==> Normalize:
[-1.00, 0.00, 0.00, 0.00,
0.00, -1.00, 0.00, 0.00,
0.00, 0.00, 1.00, 0.00,
1.00, 2.00, 3.00, 1.00]
Xform.scale_dirs()
@overload @classmethod def scale_dirs(self, xf: Sequence[float], scale: float ) -> List[float]: @overload @classmethod def scale_dirs(self, xf: Sequence[float], scale_x: float, scale_y: float, scale_z: float ) -> List[float]:
The Xform.scale_dirs() function apply a scaling factor to the directions of a transform. The origin is not changed. The scaling factor can be different for each direction or the same for all. Multiple calls are cumulative — two calls with a scale of 2.0 results in a scale of 4.0. Call Xform.normalize() to remove any scaling.
Use Xform.compose_scale() to apply a scaling factor to an axis placement, including the origin, for transforming placements between different unit systems.
Xform.transform_to()
@classmethod def transform_to(self, src: Sequence[float], dst: Sequence[float] ) -> List[float]:
The Xform.transform_to() function creates a transform that will move items in the source coordinate system to the destination system. It does this by inverting the source matrix and then composing it with the destination one. If an inverse could not be found, the function raises a value exception, as discussed by Xform.inverse().
Xform.translate()
@classmethod def translate(self, xf: Sequence[float], x: float, y: float, z: float ) -> List[float]:
The Xform.translate() function moves the origin of the transform matrix by the given distances along the directions given by the transform for the X, Y, and Z axes.
XF = step.Xform.identity() TMP = step.Xform.scale_dirs(XF, 3) print ((Simple scale:\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(TMP)) ==> Simple scale: [3.00, 0.00, 0.00, 0.00, 0.00, 3.00, 0.00, 0.00, 0.00, 0.00, 3.00, 0.00, 0.00, 0.00, 0.00, 1.00] TMP = step.Xform.scale_dirs(XF, 1, 2, 3) print ((XYZ scale:\n+[%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f,\n+%.2f, %.2f, %.2f, %.2f]) % tuple(TMP)) ==> XYZ scale: [1.00, 0.00, 0.00, 0.00, 0.00, 2.00, 0.00, 0.00, 0.00, 0.00, 3.00, 0.00, 0.00, 0.00, 0.00, 1.00]
Xform.transpose()
@classmethod def transpose(self, xf: Sequence[float] ) -> List[float]:
The Xform.transpose() function transposes the 4x4 matrix of the transform, making columns into rows and rows into columns.
XF = [ 1, 2, 3, 4,
5, 6, 7, 8,
9, 10, 11, 12,
13, 14, 15, 16 ]
XF = step.Xform.transpose(XF)
print ((Transpose:\n
+
[%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f,\n
+
%.2f, %.2f, %.2f, %.2f]
) % tuple(XF))
==> Transpose:
[1.00, 5.00, 9.00, 13.00,
2.00, 6.00, 10.00, 14.00,
3.00, 7.00, 11.00, 15.00,
4.00, 8.00, 12.00, 16.00]